链表

合并两个有序链表

将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。

示例 1：

img

1
2
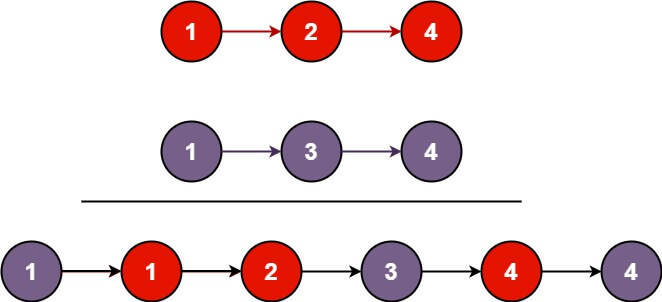
输入：l1 = [1,2,4], l2 = [1,3,4]
输出：[1,1,2,3,4,4]

示例 2：

1
2
输入：l1 = [], l2 = []
输出：[]

示例 3：

1
2
输入：l1 = [], l2 = [0]
输出：[0]

提示：

  • 两个链表的节点数目范围是 [0, 50]
  • -100 <= Node.val <= 100
  • l1 和 l2 均按 非递减顺序 排列

思路

用两个指针，分别指向两个链表头，依次比较，把更大的值添加到新链表后面，更大值所属链表的指针向前移动，合并链表指针向前移动。

注意

使用虚拟头节点可以避免空指针情况的考虑，循环退出后要检查两个链表是否都遍历完。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
ListNode* mergeTwoLists(ListNode* list1, ListNode* list2) {
    ListNode* dummy = new ListNode();
    ListNode* p1 = list1;
    ListNode* p2 = list2;
    ListNode* p = dummy;
    
    while(p1 && p2){
        if(p1->val<p2->val) {
            p->next = p1;
            p1 = p1->next;
        }
        else{
            p->next = p2;
            p2 = p2->next;
        }
        p = p->next;
    }

    if(p1) p->next = p1;
    if(p2) p->next = p2;

    return dummy->next;
}

分隔链表

86. 分隔链表 | 力扣 | LeetCode | 🟠

给你一个链表的头节点 head 和一个特定值 x ，请你对链表进行分隔，使得所有 小于 x 的节点都出现在 大于或等于 x 的节点之前。

你应当 保留 两个分区中每个节点的初始相对位置。

示例 1：

img

1
2
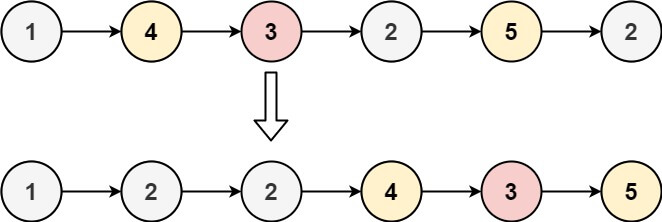
输入：head = [1,4,3,2,5,2], x = 3
输出：[1,2,2,4,3,5]

示例 2：

1
2
输入：head = [2,1], x = 2
输出：[1,2]

提示：

  • 链表中节点的数目在范围 [0, 200] 内
  • -100 <= Node.val <= 100
  • -200 <= x <= 200

思路

创建两个链表p1，p2分别保存小于x的节点和大于x的节点，用一个指针p遍历所有节点，小于x的放到p1后面，p1和p都前进一位，大于等于x的放到p2后面，p2和p都前进一位。最后把p1和p2连起来。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
ListNode* partition(ListNode* head, int x) {
    ListNode* dummy1 = new ListNode();
    ListNode* dummy2 = new ListNode();

    ListNode* p1 = dummy1;
    ListNode* p2 = dummy2;
    ListNode* p = head;

    while(p){
        if(p->val < x){
            p1->next = p;
            p1 = p1->next;
        }  
        else{
            p2->next = p;
            p2 = p2->next;
        }           
        p = p->next;
    }
    p2->next = nullptr;
    p1->next = dummy2->next;

    return dummy1->next;
}

注意

同样使用虚拟头结点保存新建的链表，p2最后要设为空，因为p1和p2的节点都是从p上直接取下的，有可能p2的后面还连着p1的节点，因此要把p2后面设为空。

合并K个有序链表

给你一个链表数组，每个链表都已经按升序排列。

请你将所有链表合并到一个升序链表中，返回合并后的链表。

示例 1：

1
2
3
4
5
6
7
8
9
10
输入：lists = [[1,4,5],[1,3,4],[2,6]]
输出：[1,1,2,3,4,4,5,6]
解释：链表数组如下：
[
  1->4->5,
  1->3->4,
  2->6
]
将它们合并到一个有序链表中得到。
1->1->2->3->4->4->5->6

示例 2：

1
2
输入：lists = []
输出：[]

示例 3：

1
2
输入：lists = [[]]
输出：[]

思路

思路和合并两个链表基本一样，差别在于用优先队列选出k个元素中的最小值。从每个链表头选出最小的元素放在返回链表的后面，把被选中链表的下一个元素放到优先队列中，返回链表指针后移，直到优先队列为空。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
ListNode* mergeKLists(vector<ListNode*>& lists) {
    if (lists.empty()) return nullptr;
    // 虚拟头结点
    ListNode* dummy = new ListNode(-1);
    ListNode* p = dummy;
    // 优先级队列，最小堆
    auto cmp = [](ListNode* a, ListNode* b) { return a->val > b->val; };
    priority_queue<ListNode*, vector<ListNode*>, decltype(cmp)> pq(cmp);
    // 将 k 个链表的头结点加入最小堆
    for (ListNode* head : lists) {
        if (head != nullptr) {
            pq.push(head);
        }
    }

    while(!pq.empty()){
        ListNode* cur = pq.top();
        pq.pop();
        p->next = cur;
        if(cur->next) pq.push(cur->next);
        p = p->next;
    }
    return dummy->next;
}

注意

  • 注意优先队列的创建，插入和取出。

删除倒数第K个节点

给你一个链表，删除链表的倒数第 n 个结点，并且返回链表的头结点。

示例 1：

img

1
2
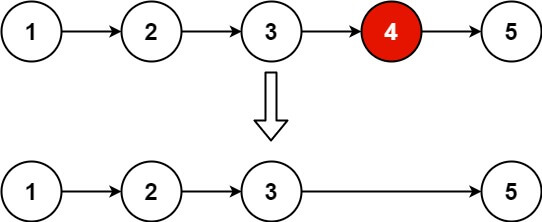
输入：head = [1,2,3,4,5], n = 2
输出：[1,2,3,5]

示例 2：

1
2
输入：head = [1], n = 1
输出：[]

示例 3：

1
2
输入：head = [1,2], n = 1
输出：[1]

思路

用两个指针，一个先走k步，再一起走。当第一个走到空时，第二个就走了n-k步，指向倒数第k个节点。不过这题是找倒数k+1个节点，所以先走k+1步。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ListNode* removeNthFromEnd(ListNode* head, int n) {
    ListNode* dummy = new ListNode();
    dummy->next = head;
    ListNode* p1 = dummy;
    ListNode* p2 = dummy;
    for(int i = 0;i<n+1;i++){
        p1 = p1->next;
    }
    while(p1){
        p1 = p1->next;
        p2 = p2->next;
    }
    p2->next = p2->next->next;
    return dummy->next;
}

注意

还是用到虚拟头结点的技巧，免去空指针的麻烦。

单链表中点&&环起点

img

img

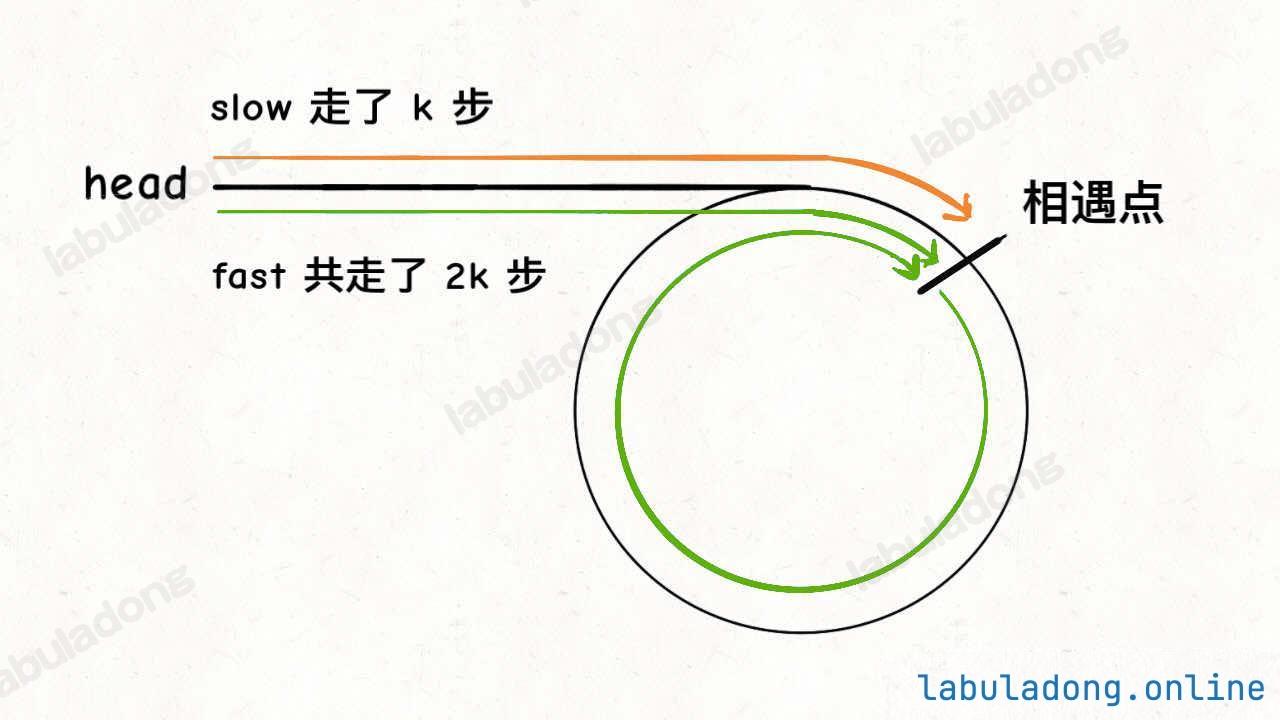
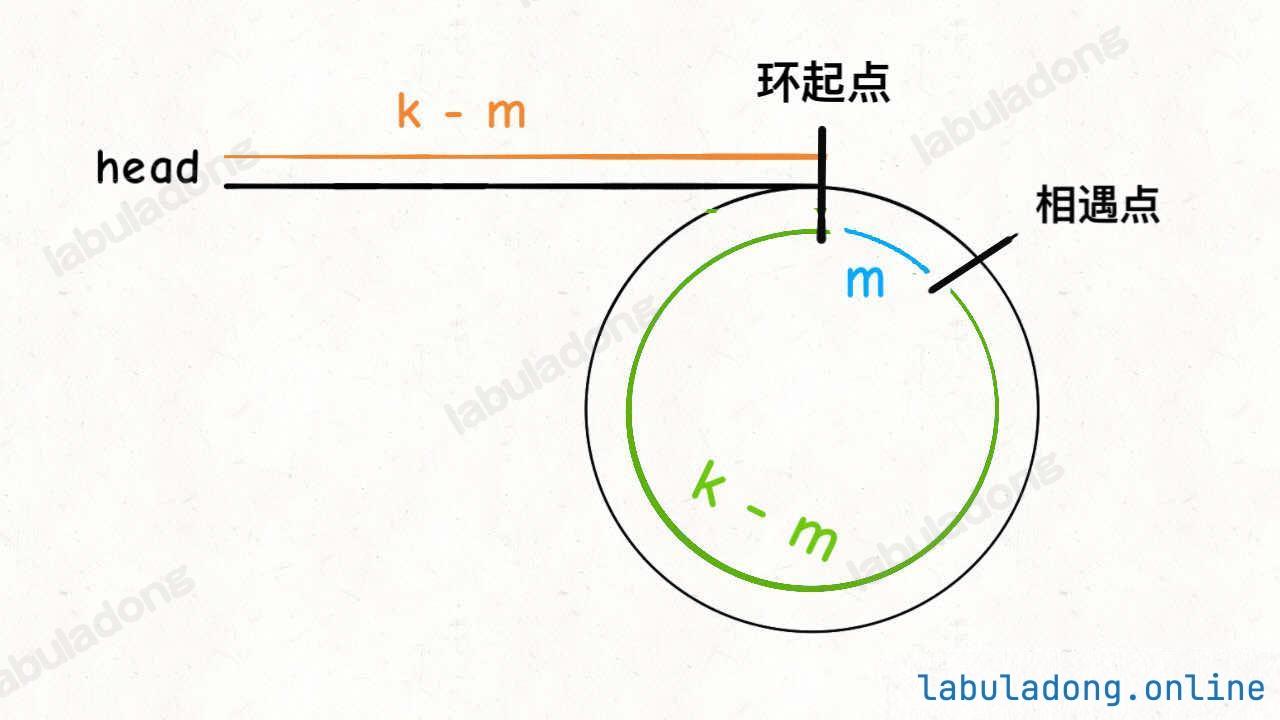
思路

当slow和fast相遇时，head到起点和fast到起点的距离是相同的。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
ListNode *detectCycle(ListNode *head) {
    if(head == NULL) return NULL;
    ListNode* slow = head;
    ListNode* fast = head;
    int cnt = 0;
    while(fast->next && fast->next->next){
        fast = fast->next->next;
        slow = slow->next;
        cnt++;
        if(slow == fast) break;
    }

    if(fast->next == NULL || fast->next->next == NULL) return NULL;
    slow = head;
    while(slow != fast) {
        fast = fast->next;
        slow = slow->next;
    }
    return fast;
}

数组

快慢指针

基本都是修改元素的题目，套路就是用两个指针，一个slow，一个fast。fast遍历所有元素，slow确保[0…slow]或者[0…slow)的元素都是满足条件的。

滑动窗口

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 滑动窗口算法伪码框架
void slidingWindow(string s) {
    // 用合适的数据结构记录窗口中的数据，根据具体场景变通
    // 比如说，我想记录窗口中元素出现的次数，就用 map
    // 如果我想记录窗口中的元素和，就可以只用一个 int
    auto window = ...

    int left = 0, right = 0;
    while (right < s.size()) {
        // c 是将移入窗口的字符
        char c = s[right];
        window.add(c);
        // 增大窗口
        right++;

        // 进行窗口内数据的一系列更新
        ...

        // *** debug 输出的位置 ***
        printf("window: [%d, %d)\n", left, right);

        // 判断左侧窗口是否要收缩
        while (窗口满足题目要求) {
            //记录当前窗口的值
            ...
            // d 是将移出窗口的字符
            char d = s[left];
            window.remove(d);
            // 缩小窗口
            left++;

            // 进行窗口内数据的一系列更新
            ...
        }
    }
}

注意

  • 选择左闭右开的窗口，这样初始化 left = right = 0 时区间 [0, 0) 中没有元素，但只要让 right 向右移动（扩大）一位，区间 [0, 1) 就包含一个元素 0 了。如果你设置为两端都开的区间，那么让 right 向右移动一位后开区间 (0, 1) 仍然没有元素；如果你设置为两端都闭的区间，那么初始区间 [0, 0] 就包含了一个元素。这两种情况都会给边界处理带来不必要的麻烦。

最小覆盖子串

给你一个字符串 s 、一个字符串 t 。返回 s 中涵盖 t 所有字符的最小子串。如果 s 中不存在涵盖 t 所有字符的子串，则返回空字符串 "" 。

注意：

  • 对于 t 中重复字符，我们寻找的子字符串中该字符数量必须不少于 t 中该字符数量。
  • 如果 s 中存在这样的子串，我们保证它是唯一的答案。

示例 1：

1
2
3
输入：s = "ADOBECODEBANC", t = "ABC"
输出："BANC"
解释：最小覆盖子串 "BANC" 包含来自字符串 t 的 'A'、'B' 和 'C'。

示例 2：

1
2
3
输入：s = "a", t = "a"
输出："a"
解释：整个字符串 s 是最小覆盖子串。

示例 3:

1
2
3
4
输入: s = "a", t = "aa"
输出: ""
解释: t 中两个字符 'a' 均应包含在 s 的子串中，
因此没有符合条件的子字符串，返回空字符串。

思路

套用模板，window是哈希表，记录了字符出现的次数。需要满足的条件是window内包含需要的所有字符，需要记录的情况是当前满足条件的子串的长度。更新的内容是window当前包含的字符数。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
string minWindow(string s, string t) {
    unordered_map<char,int> need;
    unordered_map<char,int> window;

    for(auto c:t) 
        need[c]++;

    int left = 0;
    int right = 0;

    int valid = 0;
    int start = 0;
    int len = INT_MAX;

    while(right<s.size()){
        char c= s[right];
        right++;  //左闭右开

        if(need.count(c)) {
            window[c]++;
            if(window[c] == need[c]) valid++;
        }

        while(valid == need.size()){
            if(len>right-left) { //先记录再更新
                start = left;
                len = right-left;
            }

            char d = s[left];
            if(need.count(d)){
                if(window[d] == need[d]) valid--;
                window[d]--;
            }
            left++;
        }
    }
    return len == INT_MAX?"":s.substr(start,len);
}

注意

  • window只需要记录need中存在的字符就行。
  • 用Valid记录window中满足数量条件的need字符有几个。
  • 用start和最小程度记录最小子串可以避免每次更新都要求一次子串。
  • 因为左闭右开，所以right-left就是长度。

最长无重复子串

给定一个字符串 s ，请你找出其中不含有重复字符的 最长 子串 的长度。

示例 1:

1
2
3
输入: s = "abcabcbb"
输出: 3 
解释: 因为无重复字符的最长子串是 "abc"，所以其长度为 3。

示例 2:

1
2
3
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b"，所以其长度为 1。

示例 3:

1
2
3
4
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke"，所以其长度为 3。
     请注意，你的答案必须是 子串 的长度，"pwke" 是一个子序列，不是子串。

思路

right向右遍历，把字符放进来，判断新加入的字符是否有重复的，如果有就让Left收缩到没有重复为止。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
int lengthOfLongestSubstring(string s) {
    unordered_map<char,int> window;

    int left = 0,right = 0;
    int len = 0;

    while(right<s.size()){
        char c = s[right];
        right++;

        while(window[c]>0){
            char d = s[left];
            window[d]--;
            left++;
        }
        len = max(len,right-left); //无论本次放入的有没有重复，进行到这一步时，[left...right-1]都是满足条件的子串。
        window[c]++;
    }

    return len;
}

注意

  • 对左开右闭的理解
  • map.count()是返回有没有键，map[]是返回这个键对应的值，对于map[key]==0的键值对来说，map.count(key)是1而不是0.

二分

模板

1
2
3
4
5
6
7
8
9
10
11
12
13
void BinarySearch(Vector<int> nums,int target){
    //确定初始搜索区间
	int left = 左边起始位置;
	int right = 右边起始位置;
	
	while(终止条件){
		int mid = left+(right-left)/2;
		if(nums[mid] = target) 调整区间/返回结果;
		else if(num[mid]>target) 调整区间;
		else if(nums[mid]<target) 调整区间;
	}
	//根据终止后指针指向的位置返回结果
}

找元素

  • 初始搜索区间[left..nums.size()-1]
  • 终止条件，由于是左右闭区间，因此终止条件就是left == right+1
  • nums[mid] = target，直接返回
  • num[mid]>target，mid指向的一定不是要的值，搜索区间变为[left…mid-1]
  • num[mid]<target，mid指向的一定不是要的值，搜索区间变为[mid+1…right]
  • 结束搜索后，left==right+1，区间里已经没有值，只能返回-1
1
2
3
4
5
6
7
8
9
10
11
12
13
void BinarySearch(Vector<int> nums,int target){
	int left = 0;
	int right = nums.size()-1;
	
	while(left<=right){
		int mid = left+(right-left)/2;
		if(nums[mid] = target) return mid;
		else if(num[mid]>target) right = mid-1;
		else if(nums[mid]<target) left = mid+1;
	}
	
	return -1;
}

找左边界

  • 初始搜索区间[left..nums.size()-1]
  • 终止条件，由于是左右闭区间，因此终止条件就是left == right+1
  • nums[mid] = target，因为要找左边界，边界可能仍在左边，搜索区间变为[left…mid-1]
  • num[mid]>target，mid指向的一定不是要的值，搜索区间变为[left…mid-1]
  • num[mid]<target，mid指向的一定不是要的值，搜索区间变为[mid+1…right]
  • 结束搜索后，left==right+1，left左边的值一定小于target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BinarySearch(Vector<int> nums,int target){
	int left = 0;
	int right = nums.size()-1;
	
	while(left<=right){
		int mid = left+(right-left)/2;
		if(nums[mid] = target) right = mid-1;
		else if(num[mid]>target) right = mid-1;
		else if(nums[mid]<target) left = mid+1;
	}
	
	if(left<0||left==nums.size()) return -1;
	
	return nums[left]==target?left:-1;
}

找右边界

  • 初始搜索区间[left..nums.size()-1]
  • 终止条件，由于是左右闭区间，因此终止条件就是left == right+1
  • nums[mid] = target，因为要找右边界，边界可能仍在右边，搜索区间变为[mid+1…right]
  • nums[mid]>target，mid指向的一定不是要的值，搜索区间变为[left…mid-1]
  • nums[mid]<target，mid指向的一定不是要的值，搜索区间变为[mid+1…right]
  • 结束搜索后，left==right+1，right右边的值一定大于target
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
void BinarySearch(Vector<int> nums,int target){
	int left = 0;
	int right = nums.size()-1;
	
	while(left<=right){
		int mid = left+(right-left)/2;
		if(nums[mid] = target) left = mid+1;
		else if(num[mid]>target) right = mid-1;
		else if(nums[mid]<target) left = mid+1;
	}
	
	if(right<0||right==nums.size()) return -1;
	
	return nums[right]==target?right:-1;
}

刷题

611. 有效三角形的个数

给定一个包含非负整数的数组 nums ，返回其中可以组成三角形三条边的三元组个数。

示例 1:

1
2
3
4
5
6
输入: nums = [2,2,3,4]
输出: 3
解释:有效的组合是: 
2,3,4 (使用第一个 2)
2,3,4 (使用第二个 2)
2,2,3

示例 2:

1
2
输入: nums = [4,2,3,4]
输出: 4

法一：排序&&二分

​ 排序后，用三个指针i，j，k分别指向小中大三个边长，这样只要满足nums[k]<nums[i]+nums[j]就是符合要求的三角形边长组合。可以用两个指针遍历i和j，用二分查找满足nums[k]<nums[i]+nums[j]的下标最大的k。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
int triangleNumber(vector<int>& nums) {
	int n = nums.size();
	int ans = 0;
	sort(nums.begin(),nums.end());
    
	for(int i = 0;i<n;i++){
		for(int j = i+1;j<n;j++){
			
			int left = j+1;
			int right = n-1;
			int target = nums[i]+nums[j];
			while(left<=right){
				int mid = left+(right-left)/2;
				if(nums[mid]<nums[i]+nums[j]) left = mid+1;
				else right = mid-1;
			}
			
			ans += (left-1)-(j+1)+1;
		}
	}
	return ans;

}
  • 初始搜索区间[j+1..nums.size()-1]
  • 终止条件，由于是左右闭区间，因此终止条件就是left == right+1
  • nums[mid] = target，因为要找右边界，边界可能仍在右边，搜索区间变为[mid+1…right]
  • num[mid]>target，mid指向的一定不是要的值，搜索区间变为[left…mid-1]
  • num[mid]<target，mid指向的一定不是要的值，搜索区间变为[mid+1…right]
  • 结束搜索后，left==right+1，left左边的值一定小于target。所以满足条件的下标数量是[j+1…left-1]内的数

法二：排序&&同向双指针

1
2
3
4
5
6
7
8
9
10
11
12
```

### [2389. 和有限的最长子序列](https://leetcode.cn/problems/longest-subsequence-with-limited-sum/)

给你一个长度为 `n` 的整数数组 `nums` ，和一个长度为 `m` 的整数数组 `queries` 。

返回一个长度为 `m` 的数组 `answer` ，其中 `answer[i]` 是 `nums` 中 元素之和小于等于 `queries[i]` 的 **子序列** 的 **最大** 长度 。

**子序列** 是由一个数组删除某些元素（也可以不删除）但不改变剩余元素顺序得到的一个数组。

**示例 1：**

输入：nums = [4,5,2,1], queries = [3,10,21]
输出：[2,3,4]
解释：queries 对应的 answer 如下：

  • 子序列 [2,1] 的和小于或等于 3 。可以证明满足题目要求的子序列的最大长度是 2 ，所以 answer[0] = 2 。
  • 子序列 [4,5,1] 的和小于或等于 10 。可以证明满足题目要求的子序列的最大长度是 3 ，所以 answer[1] = 3 。
  • 子序列 [4,5,2,1] 的和小于或等于 21 。可以证明满足题目要求的子序列的最大长度是 4 ，所以 answer[2] = 4 。
    1
    2
    3

    **示例 2：**

    输入：nums = [2,3,4,5], queries = [1]
    输出：[0]
    解释：空子序列是唯一一个满足元素和小于或等于 1 的子序列，所以 answer[0] = 0 。
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38



    #### 前缀和&&双指针

    虽然题目中说的是子序列的长度，但是实际要求的是长度，也就是**元素的数量**。也就是说，题目要求的是**在满足元素和小于等于query的前提下，可以从数组中选出最多多少个元素**。所以**排序后选出的数量和未排序选出的数量是一样的**。而最长的序列一定是在更小那些元素中产生，所以我们可以**用排序后的前缀和数组来找到最长的序列**。

    ```c++
    vector<int> answerQueries(vector<int>& nums, vector<int>& queries) {
        sort(nums.begin(),nums.end());
        int n = nums.size();
        vector<int> ans;
        vector<int> f(n+1,0);
        
        for(int i = 0;i<n;i++){
            f[i+1] = f[i]+nums[i];
        }

        for(auto query:queries){
            int index = lower_bound(f,query);
            ans.push_back(index);
        }
        return ans;
    }

    int lower_bound(vector<int>& nums,int target){
        int left = 0;
        int right = nums.size()-1;

        while(left<=right){
            int mid = left+(right-left)/2;
            if(nums[mid]>target) right = mid-1;
            else if(nums[mid] == target) left = mid+1;
            else left = mid+1;
        }

        return right;
    }